We present the model of populations of Markov decision processes, discuss our recent result on this model, and show an intriguing open question.
The adversarial setting
The model of populations of Markov decision processes is directly inspired by the paper Controlling a population. They consider the following question: let $A$ be a finite state system given by a set of states $Q$, a set of actions $A$, an initial state $s$, a non-deterministic transition relation $\Delta \subseteq Q \times A \times Q$, and a target state $t$. Now, let $n$ be a number of tokens (to be quantified later) initially placed on the initial state $s$; the controller is in charge of moving all the tokens to $t$. To this end, at each time step he chooses an action, which results is moving each token according to the non-deterministic transition relation. Who resolves the non-determinism? In the original paper, they consider the adversarial setting where an opponent decides how the tokens move.
The decision problem is the following: is it true that for all $n ∈ \mathbb{N},$ (number of tokens) there exists a strategy for the controller such that no matter how the adversary resolves non-determinism at each step, all tokens eventually end up in $t$? Let us formalise the notion of strategies to highlight the key difficulty that the controller must choose the same action for each token at a given time step, which becomes problematic when the tokens are spread around different states: a strategy is
$$ \sigma : (Q^n)^* \to A, $$
meaning given the history (in which state they have been along the play) of all $n$ tokens, it chooses an action. Positional strategies will always be enough: $\sigma : Q^n \to A$.
The main result of the original paper is that this problem is EXPTIME-complete, which is proved using a reduction to an exponential two-player game.
The stochastic setting
We now consider the stochastic setting where instead of an opponent, the non-determinism is resolved by randomisation. It will be clear that the exact probabilities do not matter, so for now let us say that from $q$ with action $a$ each state $p$ such that $(q,a,p) \in \Delta$ is equally likely to be chosen as next state.
The question becomes: is it true that for all $n \in \mathbb{N}$, (number of tokens) there exists a strategy for the controller such that almost surely all tokens eventually end up in $t?$
I have been working on this question since Fall 2016 when Nathalie Bertrand came to Simons to present the original paper and proposed the stochastic setting as natural continuation. After about three long years of despairs and regularly coming back at it, we (Thomas Colcombet, Pierre Ohlmann, and myself) finally made some progress and showed that the problem is decidable. Our paper is Controlling a random population (EDIT 21/12/2019: paper accepted in FoSSaCS'20).
In a few words, our solution goes as follows:
- we introduce an intermediate problem called the sequential flow problem and construct a reduction from the general problem to (many instances of) the sequential flow problem,
- we give a solution of the sequential flow problem using the max flow min cut theorem and the theory of regular cost functions.
The complexity of the algorithm we construct is not well understood, for now we only have non-elementary upper bounds. Recently Corto Mascle, Mahsa Shirmohammadi, and Patrick Totzke proved that the problem is EXPTIME-hard, leaving a sizable gap to be filled.
The polylogarithmic question
Blaise Genest (one of the author of the original paper) asked the following problem: what if now we restrict the expected number of steps before all tokens are moved to $t$, as a function of the number of tokens? To illustrate this question, let us analyse two simple examples.
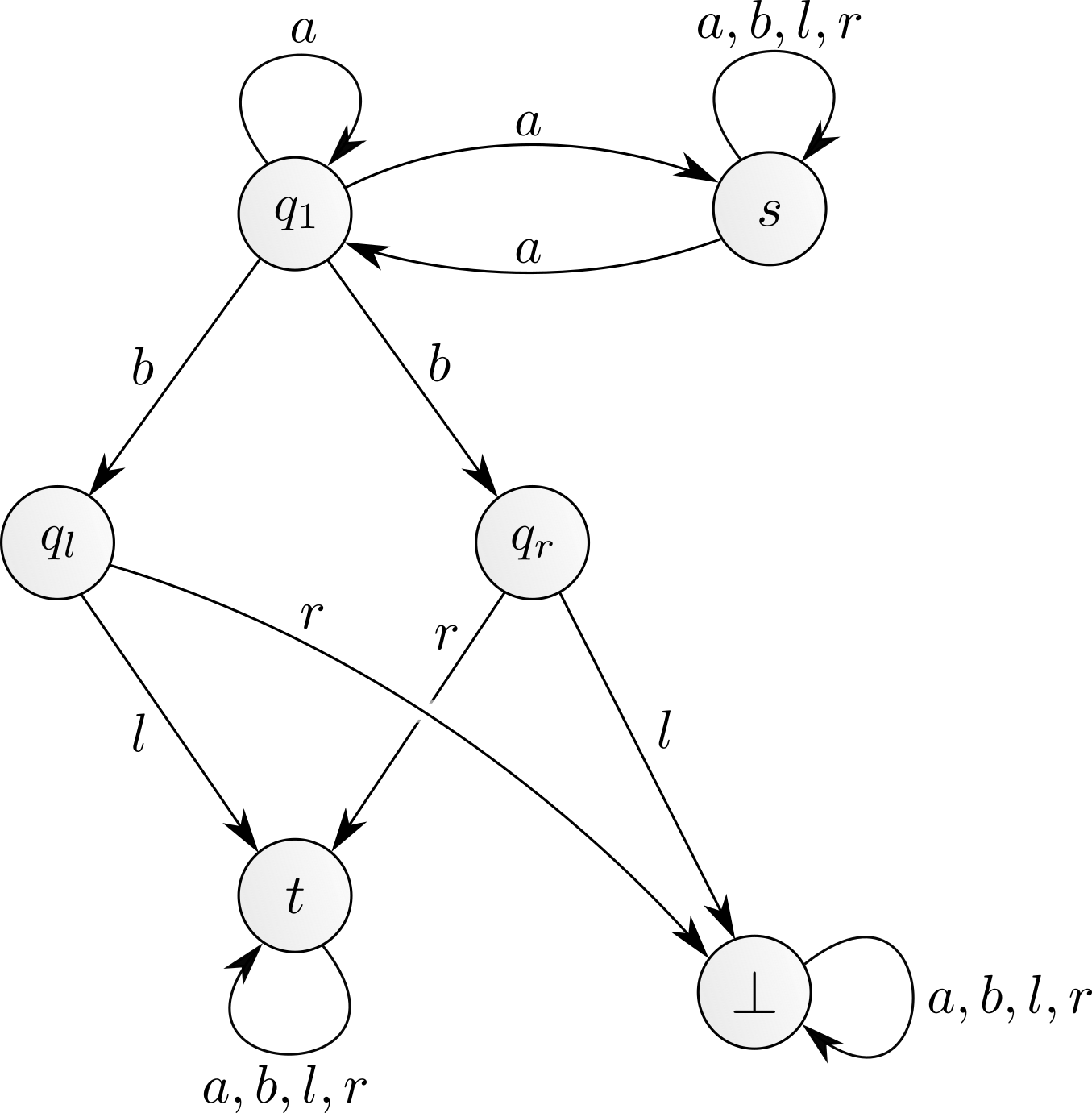
Figure 1: A first population of MDP with exponential expected synchronisation time
Let us imagine that we initially start with $n$ tokens in $s$. We can play the action $a$ a certain number of times. Each action $a$ results in reshuffling all tokens between $s$ and $q_1$. Waiting long enough, there will eventually be exactly one token in $q_1$ and $n-1$ in $s$. (Indeed this happens with probability $\frac{1}{2^n}$, so in expectation it takes $O(2^n)$ steps.) Then playing the action $b$ pushes the token either to $q_l$ or to $q_r$, and depending on this outcome playing $l$ or $r$ moves that token to $t$, while the $n-1$ other tokens quietly sit in $s$. The token safely stored in $t$ will not be further moved. Note that we could not move more than one token from $q_1$ to $t$ in this way: if we would play $b$ with two tokens in $q_1$, the risk would be that one token goes to $q_l$ and the other one to $q_r$, resulting in losing one token when choosing either $l$ or $r$. Continuing like this, we can push all tokens to $t$, one by one. This process takes a very long time, to be more precise exponential in $n$ in expectation. We say that the expected synchronisation time is exponential.
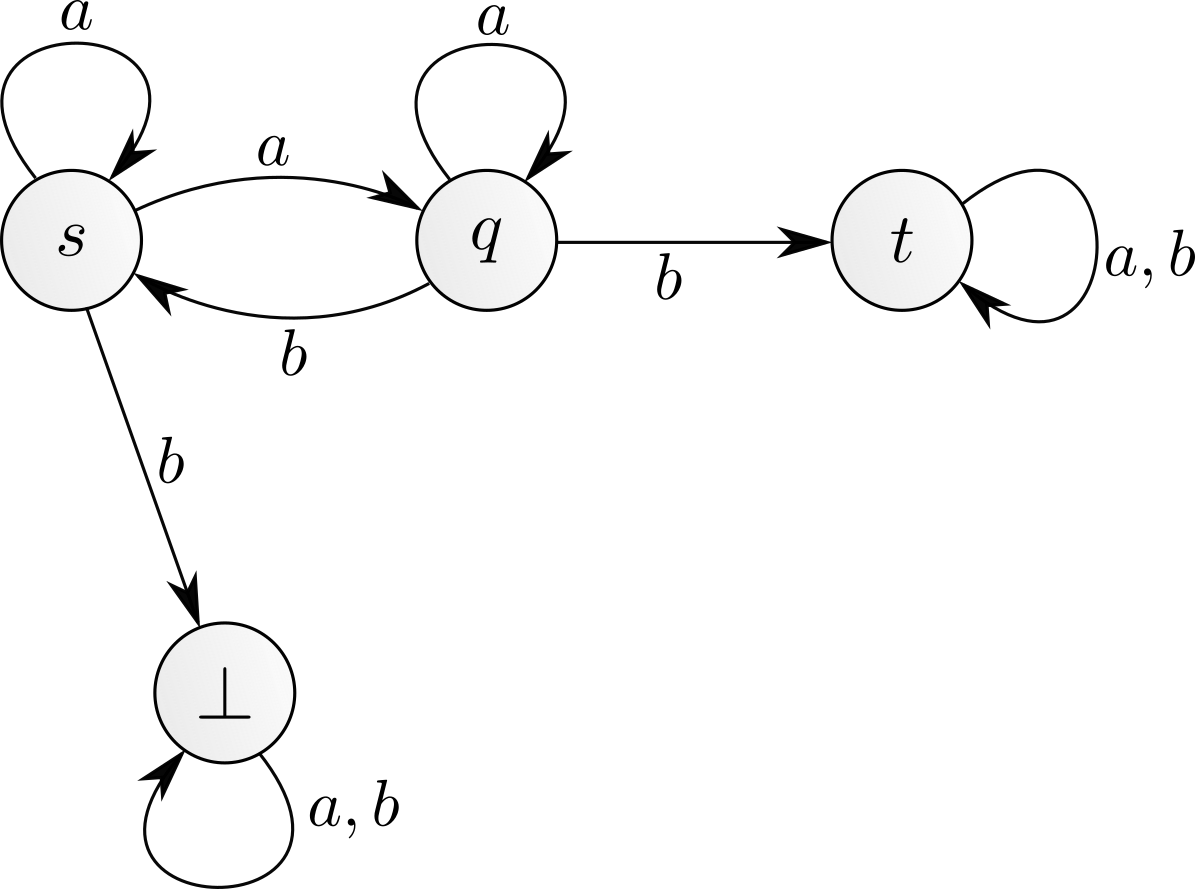
Figure 2: A second population of MDP with polylogarithmic expected synchronisation time
As before, let us start with $n$ tokens in $s$. We can play the action $a$ a certain number of times. In average, each $a$ results in halving the number of tokens in $s$ and moving half to $q$. So in expectation in a logarithmic number of steps, all $n$ tokens will be in $q$. Playing the action $b$ from there moves (in expectation) half of the tokens back to $s$ and the other half to $t$. The tokens in $t$ are safe, but now half of the tokens are back to the original state $s:$ repeating this process a logarithmic number of times we will indeed move all tokens to $t$. The expected synchronisation time is $O(\log(n)^2)$, ie polylogarithmic.
We believe that there are three interesting regimes for the expected synchronisation time:
- polylogarithmic
- polynomial
- exponential (which can be shown to be the general case)
The main open question is whether the first two cases are decidable (the third is what our paper above solves). To spell out the decision problem: given an MDP, is it true that for all $n \in \mathbb{N}$, there exists a strategy for the controller such that almost surely all tokens eventually end up in $t$, and the expected synchronisation time is bounded by $\log^{O(1)}(n)?$
Despite having spent an indecent amount of time, we (Blaise Genest, Pierre Ohlmann, myself, and some others) do not know much, but we have a very nice conjecture. It says that the problem is solved by an algorithm I studied in my PhD in a slightly different context and that we called the Markov monoid algorithm (MMA). The original goal of this algorithm was to (partially) solve the value 1 problem for probabilistic automata. (Partially because the general problem is undecidable.) Our first result was that the MMA solves the value 1 problem for the subclass of probabilistic leaktight automata, see the paper. I will not define the MMA here, I refer to the paper above, see also this blog post which constructs a similar algorithm for a different semiring.
To see the connection with probabilistic automata, let us first note that syntactically MDP and probabilistic are the exact same thing. The difference is that with an MDP we consider strategies which make decisions (choosing an action) at each step based on the current state, while probabilistic automata read words, which can be thought of as strategies not having any information on the current state.
For a word $w \in A^*$, we let $P_M(w)$ the probability that reading the word $w$ from $s$ leads to $t$. The value 1 problem asks the following question: given an MDP $M$, is it true that
$$ \forall \varepsilon > 0, \exists w \in A^*,\ P_M(w) > 1 - \varepsilon $$
Conjecture: Given an MDP $M$, the following are equivalent:
- The expected synchronisation time of polylogarithmic
- For all $\varepsilon > 0$, there exists $w$ a word of length at most $O(\log(\frac{1}{\varepsilon}))$ such that $P_M(w) > 1 - \varepsilon$
- The MMA answers YES
We (Pierre Ohlmann and myself) know that $\frac{2}{3}$ of the conjecture holds:
- the first and the second properties are equivalent
- the third property implies the second property (hence the first as well), which was proved in this paper (see also the journal version)
The difficulty is in proving that the second property implies the third. The conjecture would yield a PSPACE algorithm, and since there is a simple PSPACE lower bound, this would settle the complexity of this problem.